13 Intro to Algorithms

13 算法入门

Hi, I'm Carrie Anne, and welcome to CrashCourse Computer Science!

嗨，我是 Carrie Anne，欢迎收看计算机科学速成课！

Over the past two episodes, we got our first taste of programming in a high-level language,

前两集，我们"初尝"了高级编程语言，

like Python or Java.

比如 Python 和 Java

We talked about different types of programming language statements

我们讨论了几种语句

like assignments, ifs, and loops -

赋值语句，if 语句，循环语句

as well as putting statements into functions that perform a computation,

以及把代码打包成 "函数"

like calculating an exponent.

比如算指数

Importantly, the function we wrote to calculate exponents is only one possible solution.

重要的是，之前写的指数函数，只是无数解决方案的一种

There are other ways to write this function

还有其它方案

using different statements in different orders -

用不同顺序写不同语句

that achieve exactly the same numerical result.

也能得到一样结果

The difference between them is the algorithm,

不同的是 "算法"，意思是：

that is the specific steps used to complete the computation.

解决问题的具体步骤

Some algorithms are better than others even if they produce equal results.

即使结果一致，有些算法会更好

Generally, the fewer steps it takes to compute, the better it is,

一般来说，所需步骤越少越好

though sometimes we care about other factors, like how much memory it uses.

不过有时我们也会关心其他因素，比如占多少内存

The term algorithm comes from Persian polymath Muhammad ibn Musa al-Khwarizmi

算法 一词来自 波斯博识者 阿尔·花拉子密

who was one of the fathers of algebra more than a millennium ago.

1000 多年前的代数之父之一

The crafting of efficient algorithms

如何想出高效算法

a problem that existed long before modern computers -

是早在计算机出现前就有的问题

led to a whole science surrounding computation,

诞生了专门研究计算的领域，

which evolved into the modern discipline of...

然后发展成一门现代学科

you guessed it!

你猜对了！

Computer Science!

计算机科学！

One of the most storied algorithmic problems in all of computer science is sorting

记载最多的算法之一是"排序"

as in sorting names or sorting numbers.

比如给名字、数字排序

Computers sort all the time.

排序到处都是

Looking for the cheapest airfare,

找最便宜的机票

arranging your email by most recently sent,

按最新时间排邮件

or scrolling your contacts by last name

按姓氏排联系人

You might think

你可能想

sorting isn't so tough how many algorithms can there possibly be?

排序看起来不怎么难… 能有几种算法呢？

The answer is: a lot.

答案是超多

Computer Scientists have spent decades inventing algorithms for sorting,

计算机科学家花了数十年发明各种排序算法

with cool names like Bubble Sort and Spaghetti Sort.

还起了酷酷的名字，"冒泡排序"、"意面排序"

Let's try sorting!

我们来试试排序！

Imagine we have a set of airfare prices to Indianapolis.

试想有一堆机票价格，都飞往 印第安纳波利斯 (美国地名)

We'll talk about how data like this is represented in memory next week,

数据具体怎么在内存中表示 下周再说

but for now, a series of items like this is called an array.

上图的这样一组数据 叫"数组"（Array）

Let's take a look at these numbers to help see how we might sort this programmatically.

来看看怎么排序

We'll start with a simple algorithm.

先从一种简单算法开始

First, let's scan down the array to find the smallest number.

先找到最小数，

Starting at the top with 307.

从最上面的 307 开始

It's the only number we've seen, so it's also the smallest.

因为现在只看了这一个，所以它是最小数

The next is 239, that's smaller than 307,

下一个是 239，比 307 小

so it becomes our new smallest number.

所以新的最小数变成 239

Next is 214, our new smallest number.

下一个是 214 ，新的最小数

250 is not, neither is 384, 299, 223 or 312.

250 不是，384， 299， 223， 312 都不是

So we've finished scanning all numbers,

现在扫完了所有数字

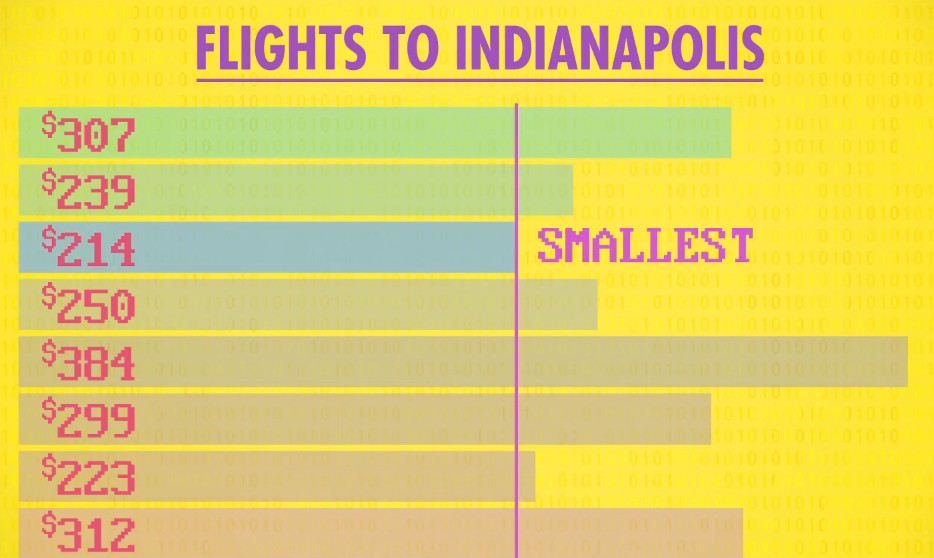
and 214 is the smallest.

214 是最小的

To put this into ascending order,

为了升序排列（从小到大排序）

we swap 214 with the number in the top location.

把 214 和最上面的数字，交换位置

Great! We sorted one number!

好棒！ 刚排序了一个数字！

Now we repeat the same procedure,

现在重复同样的过程

but instead of starting at the top, we can start one spot below.

这次不从最上面开始，从第 2 个数开始

First we see 239, which we save as our new smallest number.

先看到 239，我们当作是 "最小数"

Scanning the rest of the array, we find 223 is the next smallest,

扫描剩下的部分，发现 223 最小

so we swap this with the number in the second spot.

所以把它和第 2 位交换

Now we repeat again, starting from the third number down.

重复这个过程，从第 3 位数字开始

This time, we swap 239 with 307.

让 239 和 307 互换位置

This process continues until we get to the very last number,

重复直到最后一个数字

and voila, the array is sorted and you're ready to book that flight to Indianapolis!

瞧，数字排好了，可以买机票了！

The process we just walked through is one way

刚刚这种方法，

or one algorithm for sorting an array.

或者说算法，

It's called Selection sort and it's pretty basic.

叫 选择排序 非常基础的一种算法

Here's the pseudo-code.

以下是"伪代码"

This function can be used to sort 8, 80, or 80 million numbers

这个函数可以排序8个， 80个或8千万个数字

and once you've written the function, you can use it over and over again.

函数写好了就可以重复使用

With this sort algorithm, we loop through each position in the array, from top to bottom,

这里用循环 遍历数组

and then for each of those positions,

每个数组位置都跑一遍循环，

we have to loop through the array to find the smallest number to swap.

找最小数然后互换位置

You can see this in the code, where one FOR loop is nested inside of another FOR loop.

可以在代码中看到这一点，（一个 for 循环套另一个 for 循环）

This means, very roughly, that if we want to sort N items, we have to loop N times,

这意味着，大致来说，如果要排 N 个东西，要循环 N 次，

inside of which, we loop N times, for a grand total of roughly N times N loops, or N squared.

每次循环中再循环 N 次，共 N*N， 或 N

This relationship of input size to the number of steps the algorithm takes to run

算法的 输入大小 和 运行步骤 之间的关系

characterizes the complexity of the Selection Sort algorithm.

叫算法的 复杂度

It gives you an approximation of how fast, or slow, an algorithm is going to be.

表示运行速度的量级

Computer Scientists write this order of growth in something known as no joke -

计算机科学家们把算法复杂度叫 没开玩笑

big O notation.

大 O 表示法

N squared is not particularly efficient.

算法复杂度 O(N ) 效率不高

Our example array had n = 8 items, and 8 squared is 64.

前面的例子有 8 个元素（n=8）， 8 = 64

If we increase the size of our array from 8 items to 80,

如果 8 个变 80 个

the running time is now 80 squared, which is 6,400.

运行时间变成 80 = 6400

So although our array only grew by 10 times from 8 to 80 -

虽然大小只增长了 10 倍（8 到 80）

the running time increased by 100 times from 64 to 6,400!

但运行时间增加了 100 倍！（64 到 6400 ）

This effect magnifies as the array gets larger.

随着数组增大，对效率的影响会越来越大

That's a big problem for a company like Google,

这对大公司来说是个问题，比如 谷歌

which has to sort arrays with millions or billions of entries.

要对几十亿条信息排序

So, you might ask,

作为未来的计算机科学家你可能会问：

as a burgeoning computer scientist, is there a more efficient sorting algorithm?

有没有更高效的排序算法？

Let's go back to our old, unsorted array

回到未排序的数组

and try a different algorithm, merge sort.

试另一个算法 "归并排序"

The first thing merge sort does is check if the size of the array is greater than 1.

第一件事是检查数组大小是否 > 1

If it is, it splits the array into two halves.

如果是，就把数组分成两半

Since our array is size 8, it gets split into two arrays of size 4.

因为数组大小是 8，所以分成两个数组，大小是 4

These are still bigger than size 1, so they get split again, into arrays of size 2,

但依然大于 1，所以再分成大小是 2 的数组

and finally they split into 8 arrays with 1 item in each.

最后变成 8 个数组，每个大小为 1

Now we are ready to merge, which is how "merge sort" gets its name.

现在可以"归并"了，"归并排序"因此得名

Starting with the first two arrays, we read the first and only value in them,

从前两个数组开始，读第一个（也是唯一一个）值

in this case, 307 and 239.

307 和 239

239 is smaller, so we take that value first.

239 更小，所以放前面

The only number left is 307, so we put that value second.

剩下的唯一数字是 307 ，所以放第二位

We've successfully merged two arrays.

成功合并了两个数组

We now repeat this process for the remaining pairs, putting them each in sorted order.

重复这个过程，按序排列

Then the merge process repeats.

然后再归并一次

Again, we take the first two arrays, and we compare the first numbers in them.

同样，取前两个数组，比较第一个数

This time its 239 and 214.

239 和 214

214 is lowest, so we take that number first.

214 更小，放前面

Now we look again at the first two numbers in both arrays: 239 and 250.

再看两个数组里的第一个数：239 和 250

239 is lower, so we take that number next.

239 更小，所以放下一位

Now we look at the next two numbers: 307 and 250.

看剩下两个数：307 和 250

250 is lower, so we take that.

250 更小，所以放下一位

Finally, we're left with just 307, so that gets added last.

最后剩下 307 ，所以放最后

In every case, we start with two arrays,

每次都以 2 个数组开始

each individually sorted, and merge them into a larger sorted array.

然后合并成更大的有序数组

We repeat the exact same merging process for the two remaining arrays of size two.

我们把刚隐藏起来的，下面的数组也这样做

Now we have two sorted arrays of size 4.

现在有两个大小是 4 的有序数组

Just as before, we merge,

就像之前，

comparing the first two numbers in each array, and taking the lowest.

比较两个数组的第一个数，取最小数

We repeat this until all the numbers are merged,

重复这个过程，直到完成

and then our array is fully sorted again!

就排好了！

The bad news is: no matter how many times we sort these,

但坏消息是：无论排多少次

you're still going to have to pay $214 to get to Indianapolis.

你还是得付 214 美元到 印第安纳波利斯

Anyway, the "Big O" computational complexity of merge sort is N times the Log of N.

总之，"归并排序"的算法复杂度是 O(n * log n)

The N comes from the number of times we need to compare and merge items,

n 是需要 比较+合并 的次数

which is directly proportional to the number of items in the array.

和数组大小成正比

The Log N comes from the number of merge steps.

log N 是合并步骤的次数

In our example, we broke our array of 8 items into 4,

例子中把大小是 8 的数组，分成四个数组

then 2, and finally 1.

然后分成 2 个，最后分成 1 个

That's 3 splits.

分了 3 次

Splitting in half repeatedly like this has a logarithmic relationship with the number of items

重复切成两半，和数量成对数关系

trust me!

相信我！

Log base 2 of 8 equals 3 splits.

Log8=3

If we double the size of our array to 16 that's twice as many items to sort -

如果数组大小变成 16 之前的两倍

it only increases the number of split steps by 1

也只要多分割 1 次

since log base 2 of 16 equals 4.

因为 Log16=4

Even if we increase the size of the array more than a thousand times,

即使扩大一千倍

from 8 items to 8000 items, the number of split steps stays pretty low.

从8到8000，分割次数也不会增大多少

Log base 2 of 8000 is roughly 13.

log8000≈13

That's more, but not much more than 3 -about four times larger --

13 比 3 只是4倍多一点

and yet we're sorting a lot more numbers.

然而排序的元素多得多

For this reason, merge sort is much more efficient than selection sort.

因此"归并排序"比"选择排序"更有效率

And now I can put my ceramic cat collection in name order MUCH faster!

这下我收藏的陶瓷猫 可以更快排序了！

There are literally dozens of sorting algorithms we could review,

有好几十种排序算法，但没时间讲

but instead, I want to move on to my other favorite category of classic algorithmic problems:

所以我们来谈一个经典算法问题：

graph search!

图搜索

A graph is a network of nodes connected by lines.

图 是用线连起来的一堆 "节点"

You can think of it like a map, with cities and roads connecting them.

可以想成地图，每个节点是一个城市，线是公路

Routes between these cities take different amounts of time.

一个城市到另一个城市，花的时间不同

We can label each line with what is called a cost or weight.

可以用 成本(cost) 或 权重(weight) 来代称

In this case, it's weeks of travel.

代表要几个星期

Now let's say we want to find the fastest route

假设想找

for an army at Highgarden to reach the castle at Winterfell.

高庭到"凛冬城"的最快路线

The simplest approach would just be to try every single path exhaustively

最简单的方法是尝试每一条路

and calculate the total cost of each.

计算总成本

That's a brute force approach.

这是蛮力方法

We could have used a brute force approach in sorting,

假设用蛮力方法 来排序数组

by systematically trying every permutation of the array to check if it's sorted.

尝试每一种组合，看是否排好序

This would have an N factorial complexity

这样的时间复杂度是 O(n！)

that is the number of nodes, times one less, times one less than that, and so on until 1.

n 是节点数，n！ 是 n 乘 n-1 乘 n-2.. 一直到 1

Which is way worse than even N squared.

比 O(n)还糟糕

But, we can be way more clever!

我们可以更聪明些！

The classic algorithmic solution to this graph problem was invented by

图搜索问题的经典算法 发明者是

one of the greatest minds in computer science practice and theory, Edsger Dijkstra

理论计算机科学的伟人 Edsger Dijkstra

so it's appropriately named Dijkstra's algorithm.

所以叫 "Dijkstra 算法"

We start in Highgarden with a cost of 0, which we mark inside the node.

从"高庭"开始，此时成本为0，把0标在节点里

For now, we mark all other cities with question marks

其他城市标成问号，

we don't know the cost of getting to them yet.

因为不知道成本多少

Dijkstra's algorithm always starts with the node with lowest cost.

Dijkstra 算法总是从成本最低的节点开始

In this case, it only knows about one node, Highgarden, so it starts there.

目前只知道一个节点 "高庭"， 所以从这里开始

It follows all paths from that node to all connecting nodes that are one step away,

跑到所有相邻节点，

and records the cost to get to each of them.

记录成本

That completes one round of the algorithm.

完成了一轮算法

We haven't encountered Winterfell yet,

但还没到"凛冬城"

so we loop and run Dijkstra's algorithm again.

所以再跑一次 Dijkstra 算法

With Highgarden already checked,

高庭 已经知道了

the next lowest cost node is King's Landing.

下一个成本最低的节点，是 "君临城"

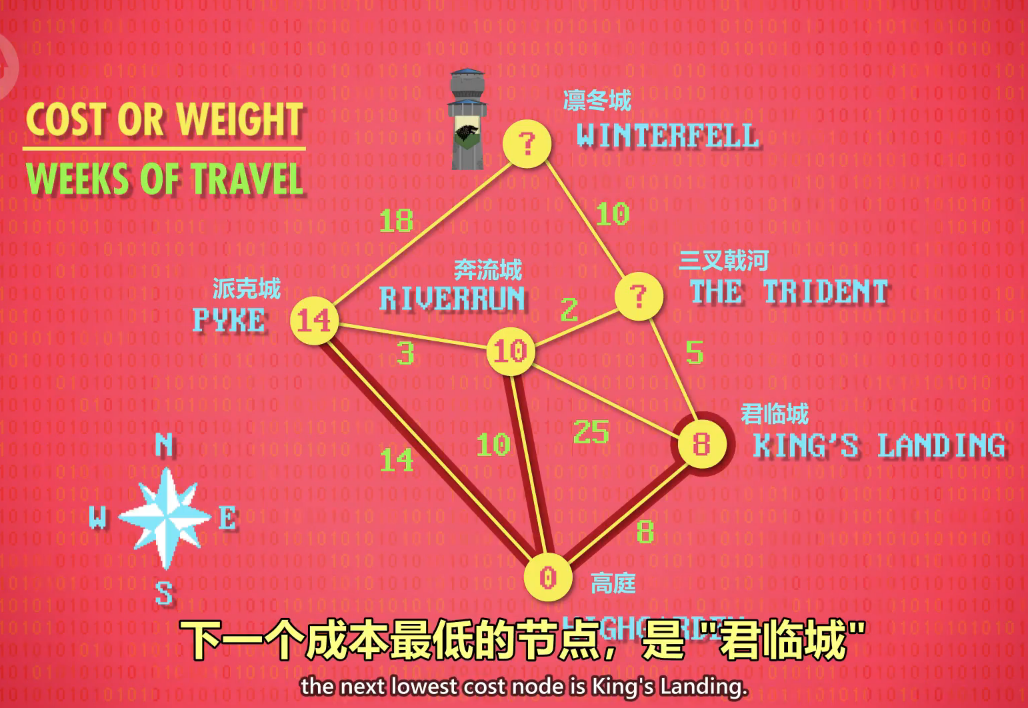
Just as before, we follow every unvisited line to any connecting cities.

就像之前，记录所有相邻节点的成本

The line to The Trident has a cost of 5.

到"三叉戟河"的成本是 5

However, we want to keep a running cost from Highgarden,

然而我们想记录的是，从"高庭"到这里的成本

so the total cost of getting to The Trident is 8 plus 5, which is 13 weeks.

所以"三叉戟河"的总成本是 8+5=13周

Now we follow the offroad path to Riverrun,

现在走另一条路到"奔流城"

which has a high cost of 25, for a total of 33.

成本高达 25 ，总成本 33

But we can see inside of Riverrun that we've already found a path with a lower cost of just 10.

但 "奔流城" 中最低成本是 10

So we disregard our new path, and stick with the previous, better path.

所以无视新数字，保留之前的成本 10

We've now explored every line from King's Landing and didn't find Winterfell, so we move on.

现在看了"君临城"的每一条路，还没到"凛冬城" 所以继续.

The next lowest cost node is Riverrun, at 10 weeks.

下一个成本最低的节点，是"奔流城"，要 10 周

First we check the path to The Trident, which has a total cost of 10 plus 2, or 12.

先看 "三叉戟河" 成本： 10+2=12

That's slightly better than the previous path we found, which had a cost of 13,

比之前的 13 好一点

so we update the path and cost to The Trident.

所以更新 "三叉戟河" 为 12

There is also a line from Riverrun to Pyke with a cost of 3.

奔流城到"派克城"成本是 3

10 plus 3 is 13, which beats the previous cost of 14,

10+3=13，之前是14

and so we update Pyke's path and cost as well.

所以更新 "派克城" 为 13

That's all paths from Riverrun checked. so you guessed it, Dijkstra's algorithm loops again.

奔流城出发的所有路径都走遍了，你猜对了，再跑一次 Dijkstra 算法

The node with the next lowest cost is The Trident

下一个成本最低的节点，是"三叉戟河"

and the only line from The Trident that we haven't checked is a path to Winterfell!

从"三叉戟河"出发，唯一没看过的路，通往"凛冬城"！

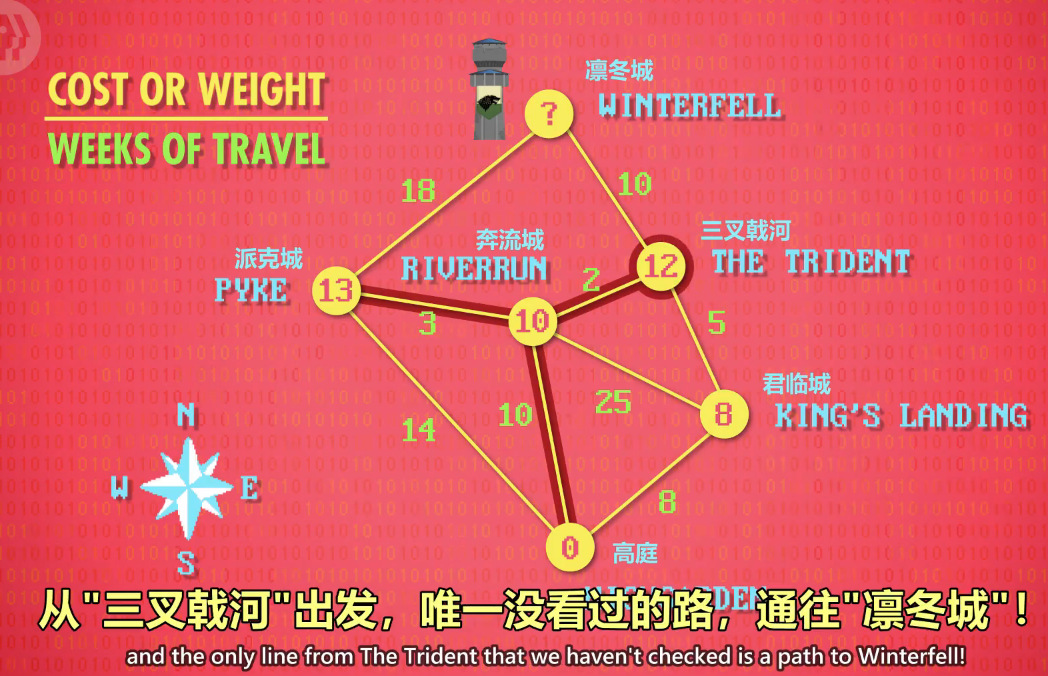
It has a cost of 10,

成本是 10

plus we need to add in the cost of 12 it takes to get to The Trident,

加"三叉戟河"的成本 12

for a grand total cost of 22.

总成本 22

We check our last path, from Pyke to Winterfell, which sums to 31.

再看最后一条路，"派克城"到"凛冬城"，成本 31

Now we know the lowest total cost, and also the fastest route for the army to get there,

现在知道了最低成本路线，让军队最快到达，

which avoids King's Landing!

还绕过了"君临城"！

Dijkstra's original algorithm, conceived in 1956,

Dijkstra 算法的原始版本，构思于 1956 年

had a complexity of the number of nodes in the graph squared.

算法复杂度是 O(n)

And squared, as we already discussed, is never great,

前面说过这个效率不够好

because it means the algorithm can't scale to big problems

意味着输入不能很大

like the entire road map of the United States.

比如美国的完整路线图

Fortunately, Dijkstra's algorithm was improved a few years later

幸运的是，Dijkstra 算法几年后得到改进

to take the number of nodes in the graph,

变成 O(n log n + l)

times the log of the number of nodes, PLUS the number of lines.

n 是节点数，l 是多少条线

Although this looks more complicated,

虽然看起来更复杂

it's actually quite a bit faster.

但实际更快一些

Plugging in our example graph, with 6 cities and 9 lines, proves it.

用之前的例子，可以证明更快，（6 个节点 9 条线）

Our algorithm drops from 36 loops to around 14.

从 36 减少到 14 左右

As with sorting,

就像排序，图搜索算法也有很多，有不同优缺点

there are innumerable graph search algorithms, with different pros and cons.

就像排序，图搜索算法也有很多，有不同优缺点

Every time you use a service like Google Maps to find directions,

每次用谷歌地图时

an algorithm much like Dijkstra's is running on servers to figure out the best route for you.

类似 Dijkstra 的算法就在服务器上运行，找最佳路线

Algorithms are everywhere

算法无处不在

and the modern world would not be possible without them.

现代世界离不开它们

We touched only the very tip of the algorithmic iceberg in this episode,

这集只触及了算法的冰山一角

but a central part of being a computer scientist

但成为计算机科学家的核心

is leveraging existing algorithms and writing new ones when needed,

是根据情况合理决定 用现有算法 还是自己写新算法

and I hope this little taste has intrigued you to SEARCH further.

希望这集的小例子能让你体会到这点

I'll see you next week.

下周见